
Here, we champion this little-known mathematics scholar with the help of a tremendous amount of internet sleuthing. While this article is certainly in answer to Seymour’s challenge from 25 years ago, our fascination with Sykes and her story is due even more to our admiration and awe at the breadth and depth of the collection of problems she created for her Source Bo ok. Had she completed a Ph.D., she would have garnered some attention, at the very least as a statistic in Judy Green and Jeanne LaDuke's 2009 Pioneering Women in American Mathematics: The Pre-1940 PhD’s. Even now, she has not been profiled in any history of mathematics books or websites with a focus on women in mathematicians. His query reflected the reality that in the pre-internet era biographical information on minor figures in the history of mathematics, such as Sykes, was not easily found. In the reprint's preface, publisher Dale Seymour challenged readers to investigate Mabel Sykes so that his press could share any uncovered information. It was through this reprinting that we learned of and became intrigued with Mabel Sykes. As a testament to its continued relevance, this book was reprinted in 1994. In her preface Sykes offered the understatement, “Hitherto much material from geometric designs or historic ornament suitable for class use could be obtained only by long and careful search through widely scattered sources.” The compilation she created went well beyond surmounting these obstacles. Published in 1912, Mabel Sykes’ A Source Book of Problems for Geometry Base d up on Industrial Design and Architectural Ornamentis an amazing example of scholarship that accomplishes this feat. Now imagine the level of scholarship necessary to do this a century ago, without our ease of travel and communication, not to mention our embarrassment of online resources. Imagine the effort required to compile nearly 2000 exercises and 500 illustrations based on over one hundred such structures around the globe. We also provide GeoGebra applets to illustrate several of these designs.Īs a real-world source for problems in Euclidean geometry, iconic buildings with ornate design-such as the Alhambra in Spain, the Taj Mahal in India, the Library of Congress in Washington, DC, or Westminster Abbey in England-offer interesting examples of shape and symmetry. We share her biography and highlight her incredible compendium of geometry problems based on architectural design.
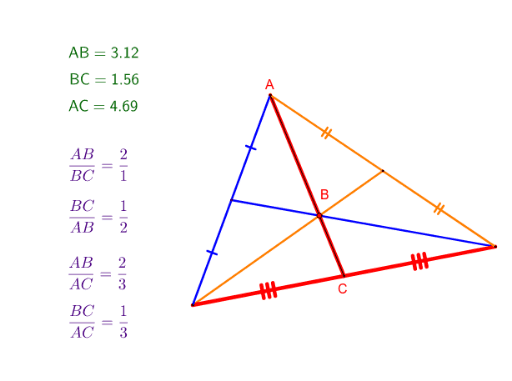
She authored textbooks and journal articles and served the greater mathematical community while teaching for almost four decades in the public school system. Similarly draw one more median to get the location of the centroid.Mabel Sykes (1868–1938) was a high-school mathematics teacher in Chicago at the start of the twentieth century. We just have to unhide the midpoints(if you had kept them hidden).Īfter they are visible again, use the Segment tool to connect a vertex with the midpoint on the opposite side. But we have already done that in the second step, we used the midpoints to draw the nine-point circle. So first we can use the Midpoint or Center tool to find/mark the midpoints on the sides. But we can use the Segment tool to draw a median.Ī median is a line segment joining a vertex to the midpoint on the opposite side.
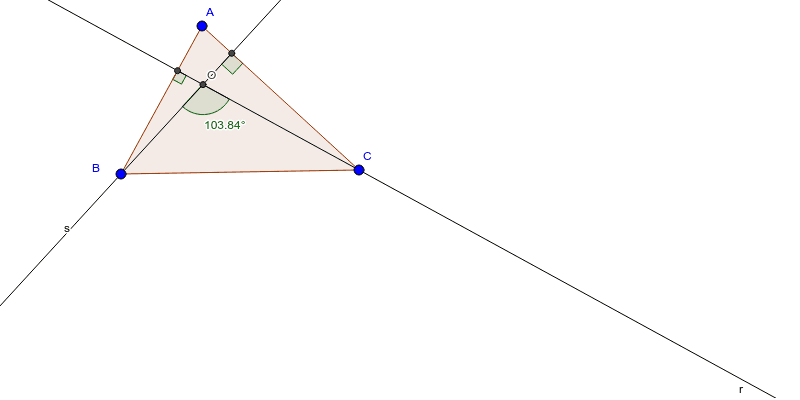
I did not find a tool that will help us directly draw a median like the Perpendicular Line tool for an altitude. Centroid is the point where the three medians of a triangle intersect. You can hide the altitudes after you have marked the orthocenter. Mark this point using the Intersect tool in the basic tools section and clicking on the two altitudes.
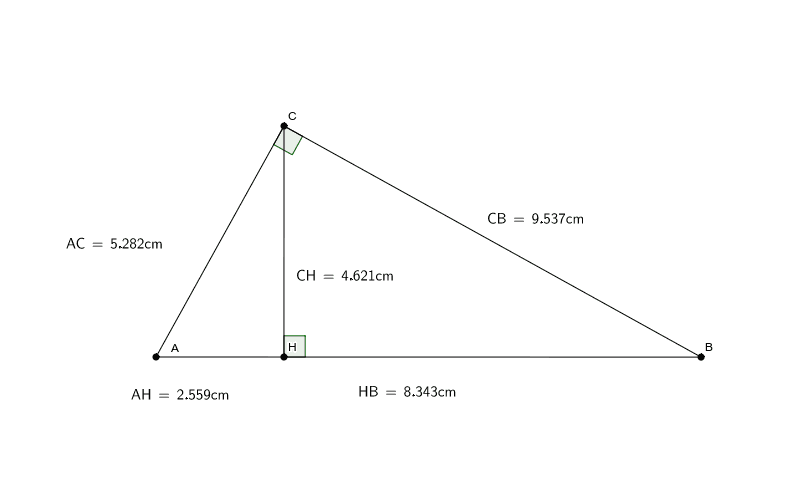
The third altitude will also pass through the same point but we don’t need to draw it as we already have found out where they are intersecting. To find the midpoint of any side, say AB, just click on the vertices A and B in any order.
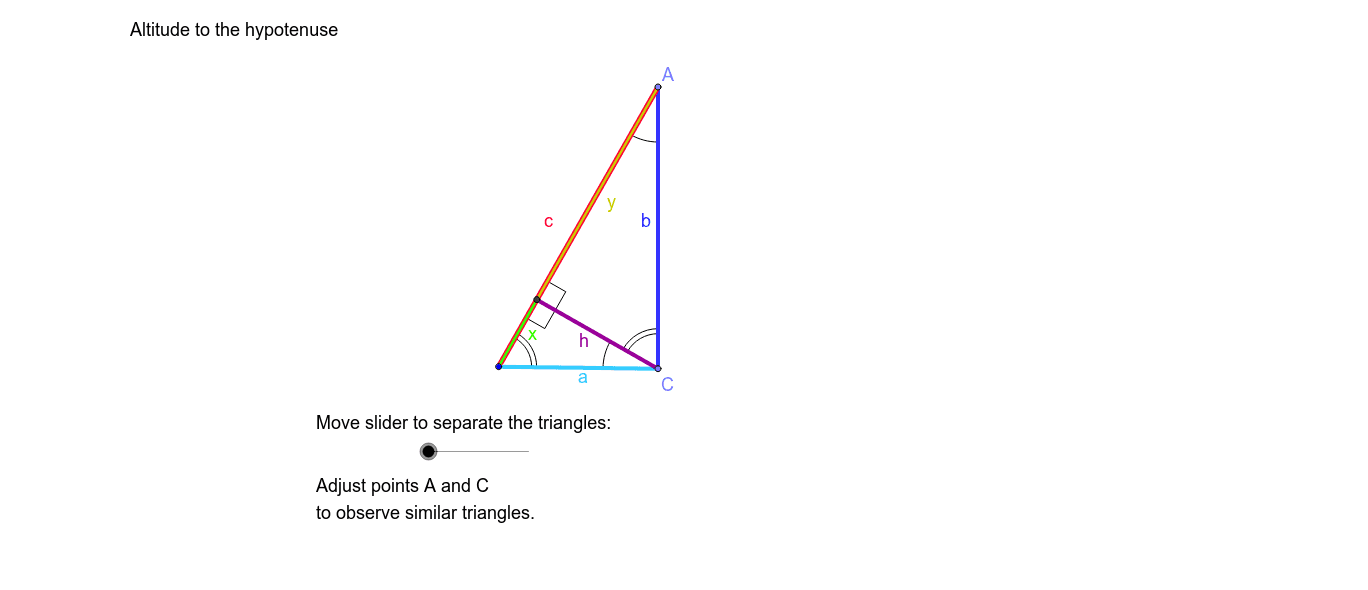
Once this tool is selected, find the midpoints of the three sides of your triangle. Select the tool Midpoint or Center under the Construct section. Since midpoints are the easiest to find we will use them to draw this circle. Any three of them will do because only three points(non-collinear) are needed to construct a circle. Midpoints of line segments from the vertices to the orthocenter of the triangle.īut to draw the nine-point circle, we don’t require all of the nine points. The nine-point circle of a triangle is a circle passing through the following nine points : But first we are going to need the nine-point circle whose center is the nine-point center. Step 2 : Constructing the nine-point center. (I have kept the axes and the grid hidden in the graph for the clarity of picture) Click again on the first point you made to finish forming the triangle. This is probably the easiest way to draw any casual triangle. To draw a triangle, click on any three different spots in the graphing panel to the right to mark the locations of the three vertices of the triangle.


 0 kommentar(er)
0 kommentar(er)
